希望不會因為連假而斷了鐵人30!

什麼是堆積

堆積（Heap）是一種資料結構，具有重要的特性，通常用於實現優先佇列（Priority Queue）以及在排序算法中的應用，例如堆排序（Heap Sort）。
堆積是一種特殊的樹狀結構，它必須滿足以下兩個關鍵特點，才能真正被稱為堆積：

1.堆積性質（Heap Property）：在最小堆（Min Heap）中，每個父節點的值都小於或等於其子節點的值；在最大堆（Max Heap）中，每個父節點的值都大於或等於其子節點的值。這保證了最小堆中的根節點具有最小值，而最大堆中的根節點具有最大值。

2.完全二元樹特性（Complete Binary Tree）：堆積必須是完全二元樹，這表示除了最低層節點外，其他層節點都必須被填滿。這一特性確保了堆積的結構緊湊且高效。

要怎麼表示它

為了實現堆，通常會使用鍊錶（linked list）或陣列（array）來表示堆的樹狀結構，並遵循特定的插入、刪除和堆化（heapify）操作，以保持堆屬性。

基本操作

前情提要

1. 每次新增或移除一個節點，都會將該節點放到根節點並根據值進行節點交換，以維護堆屬性（最小堆或最大堆屬性）。這個操作稱為堆化（Heapify）。每次堆化需要從根節點比較到葉子節點，時間複雜度為O(logN)，其中N是堆的大小。
2. 因為 Heap 是完全二元樹，代表其排列資料是緊密排列，所以可以用陣列來做實作：
   
   由上圖可以觀察出，假設現在在的節點 為 i

• 左子節點索引：leftChild = 2i + 1
• 右子節點索引：rightChild = 2i + 2
• 父節點索引：parent = (i - 1) / 2（取整數部分）

3. 我以Min Heap 來做一個說明。

建立最小堆積（Min Heap）

1.新元素首先被添加到堆積的底部（數組的末尾）。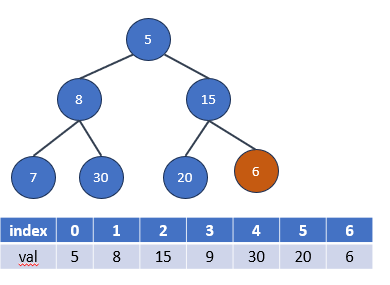

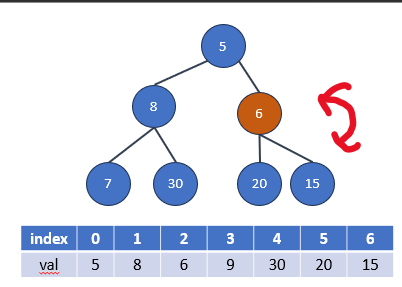
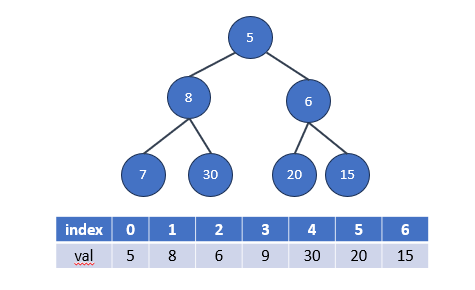
2. 然後，新元素將與其父節點進行比較。如果新元素小於其父節點，則它們交換位置。
   
3. 進行交換後，新元素再次與其新的父節點進行比較，並持續執行這個過程，直到滿足堆積性質為止。
   

刪除任意元素（Deletion）

1.首先，找到要刪除的數值在最小堆中的索引。這通常需要遍歷整個堆，以找到具有該數值的節點，並記錄其索引。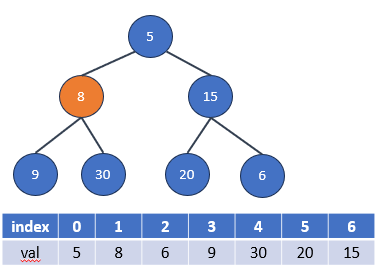

2.將要刪除的節點與堆的最後一個節點進行交換。這是為了確保刪除操作不會破壞堆的完全二元樹特性。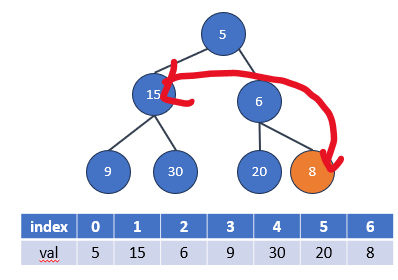

3.刪除最後一個節點，即將其從堆中移除。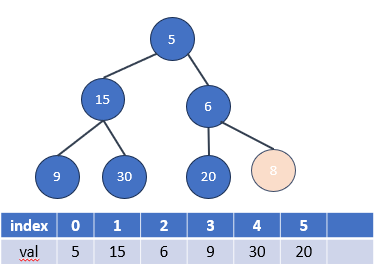

4.現在，您需要考慮兩種情況：
- 如果交換後的新節點值小於其父節點的值，則應該向上調整（使用heapifyUp操作），將新節點上移到適當的位置，以確保最小堆性質。
- 如果交換後的新節點值大於或等於其父節點的值，則應該向下調整（使用heapifyDown操作），將新節點下移到適當的位置，同樣確保最小堆性質。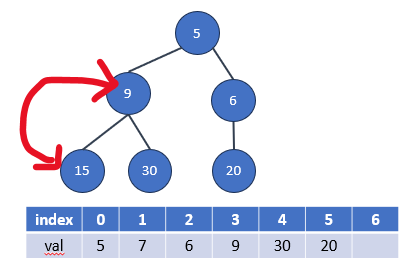

完整程式碼

#include<iostream>
#include<vector>
using namespace std;

class MinHeap{
    private:
     vector<int> heap;
        // 父節點的 index = (i-1)/2
        int parent(int i){ 
            return (i-1)/2;
        }
        // 左子節點的 index = 2*i+1
        int left(int i){
            return 2*i+1;
        }
        // 右子節點的 index = 2*i+2
        int right(int i){
            return 2*i+2;
        }
        // 維持最小堆的性質
        void heapify(int i){
            int l = left(i);
            int r = right(i);
            int smallest = i;
            if(l<heap.size() && heap[l]<heap[i])
                smallest = l;
            if(r<heap.size() && heap[r]<heap[smallest])
                smallest = r;
            if(smallest != i){
                swap(heap[i],heap[smallest]);
                heapify(smallest);
            }
        }
    public:
        // 建立最小堆
        void buildHeap(vector<int> &nums){
            heap = nums;
            for(int i=heap.size()/2-1;i>=0;i--){
                heapify(i);
            }
        }
        // 取得最小值
        int getMin(){
            return heap[0];
        }
        // 取得最小值並刪除
        int extractMin(){
            int min = heap[0];
            heap[0] = heap[heap.size()-1];
            heap.pop_back();
            heapify(0);
            return min;
        }
        // 插入新值
        void insert(int val){
            heap.push_back(val);
            int i = heap.size()-1;
            while(i>0 && heap[parent(i)]>heap[i]){
                swap(heap[i],heap[parent(i)]);
                i = parent(i);
            }
        }
        // 刪除指定值
        void remove(int val){
            int i;
            for(i=0;i<heap.size();i++){
                if(heap[i]==val)
                    break;
            }
            swap(heap[i],heap[heap.size()-1]);
            heap.pop_back();
            heapify(i);
        }
        // 印出最小堆
        void print(){
            cout << "heap: ";
            for(int i=0;i<heap.size();i++){
                cout<<heap[i]<<' ';
            }
            cout<<endl;
        }
        // 印出最小堆的大小
        int size(){
            return heap.size();
        }
        // 清空最小堆
        void clear(){
            heap.clear();
        }

};
    
int main(){
    MinHeap h;
    vector<int> nums = {5,8,15,9,30,20};
    h.buildHeap(nums);
    h.print();
    cout<<"size: "<<h.size()<<endl;

    h.insert(6);
    h.print();
    cout<<"size: "<<h.size()<<endl;

    h.remove(8);
    h.print();
    cout<<"size: "<<h.size()<<endl;

    cout<<"min: "<<h.getMin()<<endl;

    cout<<"extract min: "<<h.extractMin()<<endl;

    h.print();
    cout<<"size: "<<h.size()<<endl;

    h.clear();
    h.print();



}

當我們放下自我中心，開始關心他人，關注世界的種種，我們將能夠更深刻地理解和尊重不同的觀點和生活方式。